UD5. TANGENCIAS

Un elemento es tangente a otro cuando tan sólo se tocan en un punto, llamado punto de tangencia.
Las tangencias se pueden dar entre circunferencias (exteriores e interiores) y entre rectas y circunferencias.
Los problemas de tangencias pueden buscar los siguientes objetivos:

1. Trazado de rectas tangentes a circunferencias.
2. Trazado de circunferencias tangentes conocido el radio.
3. Trazado de circunferencias tangentes sin conocer el radio.

Para trazar tangencias hay que tener claros los siguientes principios fundamentales:

• Cuando dos circunferencias son tangentes, el punto de tangencia está contenido en la linea que une sus centros.

• Cuando una recta es tangente a una circunferencia esta recta es perpendicular al radio cuyo pie es el punto de tangencia.

• El centro de una circunferencia se encuentra en la mediatriz de sus cuerdas. Dicho de otro modo:

• El lugar geométrico de los centros de las circunferencias que pasan por dos puntos es la mediatriz del segmento definido por dichos puntos, este segmento es una cuerda de dichas circunferencias.

Centro en la intersección de las mediatices f y g

lugar geométrico de los centros de las circunferencias que pasan por B y C

• El lugar geométrico de los centros de las circunferencias tangentes a dos rectas es la bisectriz del ángulo formado por estas.

Además de conocer estos principios fundamentales hemos de tener claros los siguientes lugares geométricos:

• Una circunferencia concéntrica de radio (r+s) a otra de radio (r) es el lugar geométrico de los puntos del plano que son centros de las circunferencias tangentes exteriores de radio (s) a la cicunferencia de radio (r).

• Una recta r paralela de otra recta (s) a una distancia (d) es el lugar geométrico de los puntos del plano que son centros de circunferencias de radio (d) tangentes a la recta s. 

RESOLUCIÓN DE PROBLEMAS DE TANGENCIAS

La resolución de los problemas de tangencias pasa por hallar geométricamente (no por aproximación) los puntos de tangencia y los centros de las circunferencias si la solución son estas. 

TRAZADO DE RECTAS TANGENTES

Recta tangente a una circunferencia dado el punto de tangencia T en esta.

Para hallar la recta tangente (i), hemos de dibujar una perpendicular al radio de la circunferencia en el el punto de tangencia T.

Rectas tangentes a una circunferencia desde un punto P exterior a esta.

Datos: Circunferencia y punto P exterior.

Unir el punto P con el centro de la circunferencia O.

Hallar la mediatriz del segmento PO.

Concentro en M y radio MP dibujamos una circunferencia que corta a la dada en los puntos A y B, que son los puntos de tangencia buscados.

Unir P con A y con B, las rectas t1 y t2 son las tangentes buscadas.

Recta tangente a una circunferencia de centro desconocido dado el punto de tangencia T.

Datos: Arco y punto T en él.

Unir el punto P con el centro de la circunferencia O.

Hallar la mediatriz del segmento PO.

Concentro en M y radio MP dibujamos una circunferencia que corta a la dada en los puntos A y B, que son los puntos de tangencia buscados.

Unir P con A y con B, las rectas t1 y t2 son las tangentes buscadas.

Rectas tangentes a una circunferencia paralelas a una dirección:

Datos: Dirección d y circunferencia.

Dibujar una perpendicular (i) a la recta d dada desde el centro de la circunferencia O.

Los puntos de intersección de la recta i con la circunferencia, T1 y T2 son los puntos de tangencia buscados.

Trazar las paralelas t1 y t2 por los puntos anteriormente nombrados.

 

Rectas tangentes comunes a dos circunferencias:

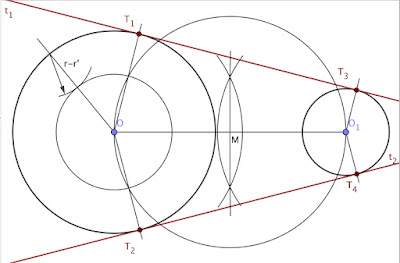
Tangentes exteriores:

Datos: Circunferencias de centros O de radio r y O’ de radio r’.

A la circunferencia mayor O le restamos el radio de la circunferencia menor, r-r’ y dibujamos la circunferencia resultante.

Hallamos la mediatriz de segmento OO’ y con centro en el punto medio M dibujamos la circunferencia auxiliar cuyo radio es MO. 

Unimos los puntos de corte de esta circunferencia auxiliar con la anterior y en su prolongación encontramos T1 y T2 puntos de tangencia buscados.

Para hallar T3 y T4 en la otra circunferencia dada tan sólo tenemos que trazar paralelas a las rectas auxiliares anteriores.

Unimos T1 con T1’ y T2 con T2’.

Tangentes interiores:

Datos: Circunferencias de centros O de radio r y O’ de radio r’.

A la circunferencia mayor O le sumamos el radio de la circunferencia menor, r+r’ y dibujamos la circunferencia resultante.

Hallamos la mediatriz de segmento OO’ y con centro en el punto medio M dibujamos la circunferencia auxiliar cuyo radio es MO. 

Unimos los puntos de corte de esta circunferencia auxiliar con la anterior y sobre O encontramos T1 y T2 puntos de tangencia buscados.

Para hallar T3 y T4 en la otra circunferencia dada tan sólo tenemos que trazar paralelas a las rectas auxiliares anteriores, pero en esta ocasión lo haremos de manera intercambiada.

Unimos T1 con T1’ y T2 con T2’.

CIRCUNFERENCIAS TANGENTES CONOCIDO EL RADIO

Circunferencias que pasan por dos puntos A y B:

Datos: Dos puntos A y B y el radio R de las circunferencias:

Concepto: El lugar geométrico de los centros de las circunferencias que pasan por dos puntos es la mediatriz de la cuerda de la cual son extremos.

1. Tan sólo hemos de dibujar la mediatriz del segmento aB, cuerda de las circunferencias buscadas.
2. Con centro en A o B y radio R trazamos sendos arcos que cortan a la mediatriz en los puntos O1 y O2, centros de las circunferencias de radio R buscadas.
3. Dibujar las circunferencias que pasan por A y B.

Circunferencias tangentes a una recta y que pasan por un punto de esta:

Datos: Radio R de la circunferencia buscada, recta r y punto contenido en ella:

1. Dibujamos la perpendicular a la recta r por el punto dado.
2. Con radio R pinchamos en el punto para hallar en la mediatriz los puntos O1 y O2, centro de las circunferencias que buscamos.
3. Dibujamos las circunferencias.

Circunferencias tangentes a una recta que pasan por un punto exterior a esta:

Datos: Radio R de la circunferencia buscada, recta r y punto A exterior:

1. Sobre una perpendicular a la recta r marcamos la distancia dada R y dibujamos una paralela a la distancia R de la recta.
2. Pinchando en A y radio R hacemos sendos arcos para encontrar sobre la paralela s los puntos O1 y O2, centros de las circunferencias.
3. Para hallar los puntos de tangencia con la recta r, dibujar perpendiculares a la recta r desde O1 y O2
4. Dibujamos las circunferencias que pasan por A y T1 y T2.

Circunferencias de radio dado que pasan por un punto y son tangentes a una circunferencia:1.- Circunferencias de radio dado R que son tangentes a otra dado el punto de tangencia T:

Datos: Radio R de las circunferencias buscadas, Circunferencia de centro O y punto de tangencia T:

concepto: Los centros de las circunferencias tangentes están alineados con el punto de tangencia.

1. Según lo anterior dibujamos una recta que una el centro O con el punto de tangencia T.
2. Con radio R pinchamos en T y hallamos sobre la recta los puntos O1 y O2, centros de las circunferencias buscadas.
3. Dibujar las circunferencias de radio R buscadas (una interior y otra exterior).

2.- Circunferencias de radio R dado tangentes a otra dada O pasando por un punto P exterior a ella:

Datos: Radio R (siendo R > r) de las circunferencias buscadas, Circunferencia de centro O y punto de tangencia T:

concepto: 

• El lugar geométrico de las circunferencias de radio R tangentes una de radio r es la circunferencia concéntrica con radio r+R y radio r-R.

• El lugar geométrico de los centros de las circunferencias de radio R que pasan por P es una circunferencia de radio R con centro en P.

Según lo anterior:

1. Dibujamos una circunferencia con centro en O y radio R+r: Para ello dibujamos un radio aleatorio de O y lo prolongamos sumando el radio R dado.
2. Para hacer la circunferencia r-R: Marcar la distancia R con centro en O hallando el punto I y con centro en I y radio r hallaremos el punto P1. OP1= R-r. Dibujamos la circunferencia OP1.
3. Para hallar los centros de las circunferencias buscadas, trazar una circunferencia de radio R y centro en P. Sus intersecciones con las dos anteriores nos dan los puntos O1, O2, O3 y O4, centros de las circunferencias buscadas.
4. Para hallar los puntos de tangencia T1…T4 uniremos los centros O1…O4 con O.
5. Dibujamos las circunferencias. Cuatro soluciones en total, dos externas que contienen a O y dos externas.

Si R<r en ese caso la solución se simplifica:

Circunferencias de radio R tangentes a dos rectas que se cortan:

Datos: Radio R de las circunferencias buscadas, par de rectas que se cortan:

concepto:

• El lugar geométrico de los centros de las circunferencias de radio R tangentes una recta es una paralela a la recta a una distancia R de ella .
• Una recta tangente a una circunferencia es perpendicular al radio cuyo pie es el punto de tangencia.

1. Según lo anterior dibujamos rectas paralelas a las dadas, los puntos de corte de dichas paralelas (O1, O2, O3 y O4) cumplirán la doble condición de encontrarse a una distancia R de ambas rectas. Son, pues, los centros de las circunferencias buscadas.
2. Para hallar los puntos de tangencia T1…T4, lanzamos perpendiculares a las rectas desde los centros de las circunferencias.

Circunferencias de radio R tangentes a una circunferencia de radio r y a una recta s dadas:

Caso 1: R<r

Datos: Radio R de las circunferencias buscadas, Circunferencia de centro O y recta s:

concepto: 

• El lugar geométrico de los centros de las circunferencias de radio R tangentes una recta es una paralela a la recta a una distancia R de ella .
• El lugar geométrico de las circunferencias de radio R tangentes una de radio r es la circunferencia concéntrica con radio r+R.

1. Según lo anterior dibujamos una recta paralela a la recta s a una distancia R.
2. Con radio R+r hacemos una circunferencia con centro O. Esa circunferencia se corta con la recta auxiliar anterior en los puntos O1 y O2, centro de las circunferencias buscadas.
3. Para hallar los puntos de tangencia T1…T4 lanzamos perpendiculares desde O1 y O2 a la recta s hallando T1 y T2. Y unimos los centros O1 y O2 para encontrar T3 y T4.

Caso 2: R>r

En este ejercicio existen 4 resultados. Los dos primeros se hallan como en el ejercicio anterior, las otras dos son exteriores que contienen a la circunferencia dada.

fig. 1

fig. 2

fig. 3

Los datos son los mismos que en el caso anterior, excepto que el radio R dado es mayor que el radio r de la circunferencia  O (R>r).

1. En el primer paso operaremos de la misma manera que en el ejercicio anterior.
2. Después restaremos al radio mayor R el menor r. Para ello dibujaremos un diámetro de la circ. O para, desde un extremo, coger la distancia de R, de tal manera que desde el centro O a la marca anterior nos quede el resultado de restar r a R (R-r) Fig. 3 y con ese radio y centro O dibujar una circunferencia auxiliar.
3. Las intersecciones de esta circunferencia con la recta auxiliar nos darán O1 y O2, centros de las circ. buscadas.
4. A partir de aquí hallamos los puntos de tangencia T1…T4 como en el ejercicio anterior y dibujamos las circunferencias.

Circunferencias de radio R dado, tangentes a otras dos circunferencias:Caso 1: R<r

Datos: Radio R de las circunferencias buscadas, circunferencias O y O’ dadas.

Concepto: El lugar geométrico de los centros de las circunferencias de radio R tangentes a las dadas es la intersección de sendas circunferencias concéntricas a las  O y O’ de radio r+R y r’+R.

1. Según lo anterior sobre la prolongación del radio r y r’ añadiremos la magnitud R y dibujamos dos circunferencias auxiliares.
2. Los puntos de intersección de estas, O1 y O2 son los centros de las circunferencias buscados.
3. Para hallar los puntos de tangencias T1…T4 unimos los centros de las circunferencias halladas con los de las dadas. 

Caso 2: R>r

En un caso como este podemos encontrar hasta 6 soluciones, si tenemos en cuenta que podemos dibujar las circunferencias tangentes externas que contienen a O, externas que contienen a O’, e incluso las externas que contendrían a O y O’ si el radio R fuera lo suficientemente grande. (Fig. 1)

Nos limitaremos por tanto a dibujar tan solo el caso de las circunferencias externas que contienen a O, por ello en vez de sumar R+r lo que haremos será restar R-r para dibujar la circunferencia auxiliar de ese radio.

Datos: Radio R de las circunferencias buscadas, circunferencias O y O’ dadas.

Concepto: El lugar geométrico de los centros de las circunferencias de radio R tangentes a las dadas es la intersección de sendas circunferencias concéntricas a las  O y O’ de radio R-r y r1+R.

1. Según lo anterior sobre la prolongación del radio r’ añadiremos la magnitud R y en la circunferencias O dada dibujaremos sobre un diámetro el radio R siendo el radio de la circunferencia auxiliar R-r: observa que en este caso la circunferencia auxiliar será interior a la dada. Una vez hecho esto dibujamos ambas circunferencias concéntricas a las dadas.
2. Los puntos de intersección de estas circunferencias auxiliares, O1 y O2, son los centros de las circunferencias buscados.
3. Para hallar los puntos de tangencias T1…T4 unimos los centros de las circunferencias halladas con los de las dadas. 

UD4. TRANSFORMACIONES GEOMÉTRICAS

Una transformación geométrica es una correspondencia entre los elementos de dos formas geométricas.

Las transformaciones geométricas pueden ser:

1. ISOMÉTRICAS (= medida): Entre la figura original y la transformada se mantienen las magnitudes lineales y los ángulos.
1. GIROS
2. TRASLACIÓN
3. SIMETRÍA
2. ISOMÓRFICAS (= forma): Mantienen la misma forma pero no el tamaño.
1. HOMOTECIA
3. ANAMÓRFICAS: Cambia el tamaño y el valor angular.
1. INVERSIÓN
2. HOMOLOGÍA
3. AFINIDAD 

HOMOTECIA

La homotecia es un tipo de transformación que relaciona los elementos de dos figuras, puntos o rectas llamados homotéticos, tal que:

1. Dos puntos homotéticos A y A' están alineados con otro punto O llamado centro de homotecia.
2. Dos rectas homotéticas a y a' son paralelas.

Razón de Homotecia:

La razón o coeficiente de homotecia es la relación que hay entre las distancias desde el centro de homotecia O a los puntos homotéticos A yA'. Es una constante llamada k.

k= OA/OA'

La homotecia puede ser directa (k>0) o inversa (k<0).

• Si la homotecia es directa los dos puntos homotéticos están al mismo lado del centro de homotecia.
• Si la homotecia es inversa los puntos homotéticos tienen interpuesto el centro de homotecia quedando uno a cada lado de O.

Para definir la homotecia basta con conocer uno de estos dos datos:

• Cetro de homotecia y dos puntos homotéticos.
• Centro y razón de homotecia.
• Dos figuras homotéticas.

TRAZADO DE HOMOTECIA DIRECTA

TRAZADO DE HOMOTECIA INVERSA

Casuística:

1.- Hallar el homotético del punto B dado conociendo  el centro de homotecia O y una pareja de puntos homotéticos A y A'.

pasos:

1. Unir B con el centro de homotecia O.
2. Dibujar la recta AB
3. Desde A' dibujar una recta paralela a la anterior
4. La intersección con la prolongación de la recta OB será B', homotético de B buscado.

2.- Dado el triángulo ABC, dibujar un cuadrado inscrito en el mismo.

SIMETRÍA

Todos hemos hecho esto alguna vez con  un espejo o un escaparate. Estamos, con esta acción, haciendo un ejercicio de simetría. La separación entre el espejo y la realidad es una línea llamada eje de simetría.

En geometría existen dos tipos de simetrías dependiendo de cual es el centro de la transformación:

1. Simetría Axial: Existe un eje de simetría que es una línea recta.
2. Simetría central: El centro de simetría es un punto.

SIMETRÍA AXIAL

En la simetría axial deben cumplirse las siguientes leyes:

1. La recta que une dos puntos simétricos A, A', es perpendicular a otra llamada eje de simetría.
2. Dos puntos simétricos A y A' están a ambos lados del eje y a la misma distancia de este.
3. Los puntos situados en el eje de simetría tienen su simétrico coincidentes con sí mismos, por ello al eje de simetría se le llama lugar geométrico de los puntos dobles.
4. Las rectas simétricas se encuentran en un punto del eje.

SIMETRÍA CENTRAL

En la simetría axial deben cumplirse las siguientes leyes:

1. La recta que une dos puntos simétricos A, A' pasa por otro O llamado centro de simetría.
2. Dos puntos simétricos A y A' están a ambos lados del centro de simetría y a la misma distancia de este.
3. Las rectas simétricas son paralelas.

TRASLACIÓN

La traslación es una transformación geométrica en la que los puntos de un objeto se mueven una distancia constante en una determinada dirección.
La traslación tiene que cumplir las siguientes reglas:

• La recta que une dos puntos homólogos es paralela a una recta d dada llamada dirección de traslación.
• Dos rectas homólogas son paralelas.
• Todos los puntos se trasladan una misma distancia en un mismo sentido.

Traslación de un polígono

GIRO

Un giro es una transformación que se realiza siempre alrededor de un punto O, centro de giro, con un ángulo y en una dirección determinada.

La traslación tiene que cumplir las siguientes reglas:

• La distancia de un punto A y su homólogo A’ con respecto al centro de giro es constante.

• En ángulo formado por una pareja de puntos homólogos cuyo vértice es el centro de giro AOA’ es igual al ángulo de giro dado.

• Todos los puntos se giran siguiendo el mismo sentido de giro.

giro de un polígono un determinado ángulo.

Los giros los realizaremos copiando repetidamente el ángulo de giro dado para cada uno de los puntos del polígono a girar.

Giro de una recta cualquiera dado el ángulo de giro

1. Operamos eligiendo dos puntos cualesquiera A y B de la recta.
2. Hallamos sus homólogos A' y B'.
3. Los unimos para obtener la recta homóloga r'.

UD3.PROPORCIONALIDAD, IGUALDAD, SEMEJANZA Y ESCALAS

Las proporciones . La igualdad entre dos razones recibe el nombre de proporción. La teoría de las proporciones fue desarrollada por el gran matemático griego Eudoxio_de_Cnidos.

Razones y proporciones

Razón

La razón es la relación entre dos números, definida como el cociente de un número por el otro. Entonces:

La razón entre dos números a y b es la fracción  y se lee a es a b. Esta razón también puede escribirse a:b.

Proporción

Dadas dos razones a/b y c/d, diremos que están en proporción si a/b = c/d, el resultado es un número al que se le llama constante (k).

Los términos a y d se denominan extremos mientras que b y c son los medios.

En toda proporción el producto de los extremos es igual al producto de los medios

a/b = c/d  ⇒  a·d = b·c 

MEDIA PROPORCIONAL ENTRE DOS SEGMENTOS:

Sean dos segmentos a y b se llama media proporcional de estos dos segmentos a un tercero x tal que: a/x = x/b.
En geometría utilizamos dos teoremas relacionados con el triángulo rectángulo para hallar esta media proporcional:

1.- Teorema del cateto:

Dice que el cateto de un triángulo rectángulo es media proporcional entre la hipotenusa y su proyección ortogonal sobre ella.

Para ver su aplicación mira este video:

2.- Teorema de la altura:

Dice que la altura de un triángulo rectángulo es media proporcional de la dos partes en que divide con su pie a la hipotenusa.

Para ver su aplicación mira este video:

TEOREMA DE TALES:

Otro teorema importante en la proporcionalidad entre segmentos es el de Tales. Ya lo vimos en el tema anterior para la división de un segmento en partes iguales.
El teorema de Tales dice que un haz de rectas paralelas determinan sobre otras dos rectas coplanarias concurrentes segmentos proporcionales entre sí. De la siguiente manera:

Utilizaremos el Teorema de Tales en muchos conceptos proporcionales relativos a segmentos. Si quieres ver como se opera con él, sigue el video:

Tercero proporcional entre dos segmentos

Sean dos segmentos a y b se trata de hallar un tercero proporcional a ellos tal que:

a/b =b/x

Siendo x el segmento buscado.

Para ello aplicaremos el teorema de Tales.

Cuarto proporcional entre dos segmentos

Sean tres segmentos a, b y c será su cuarto proporcional el segmento x tal que:

a/b=c/x

De nuevo utilizaremos el teorema de Tales para su resolución:

SECCIÓN AUREA DE UN SEGMENTO (DIVISIÓN EN SU MEDIA Y EXTREMA RAZÓN)

Se llama sección aurea de un segmento a la producida por un punto tal que el todo es a la parte mayor como la mayor es a la menor. Esto es:

Construcción:

Los segmentos d y e son los resultantes de la construcción.

Trazar un segmento AC del cual se da el Áureo AB (rectángulo áureo):

La sección áurea en el pentágono:

La Sección Áurea está muy presente en el pentágono:
La relación entre el lado f y la diagonal m cumple esta proporción.
Las alturas h1 y h2 están en la misma relación.
Y los segmentos q y r del pentágono estrellado también la cumplen.

RELACIONES GEOMÉTRICAS:

Igualdad:

Dos figuras son iguales cuando sus ángulos y sus lados respectivos son iguales.

construcción de figuras iguales:

1.- Por copia de ángulos ángulos:

2.- Por coordenadas:

3.- Por radiación:

4.- Por triangulación:

Semejanza:

Dos figuras son semejantes cuando tienen sus ángulos iguales y sus lados correspondientes proporcionales.

Se denomina razón de semejanza a la relación que existe entre los lados proporcionales de las figuras semejantes, se expresa mediante una fracción y es una constante.

Construir una figura semejante a otra a partir de la razón de semejanza:

mediante radiación:

mediante coordenadas:

Construir un polígono semejante a otro conocido el lado:

Construcción de una figura inversamente semejante:

ESCALAS

La escala es la relación de semejanza que existe entre dos figuras, la figura del dibujo y la figura real, esta relación se representa mediante un cociente. En el numerador tendremos la medida del dibujo y en denominador la medida del objeto real.

Hay tres tipos de escala:

Escala de reducción:

La utilizamos cuando la figura real es demasiado grande para ser representada dentro de la superficie de dibujo. En ella el denominador es siempre mayor que el numerador.

Escala natural:

En la escala natural se representa el objeto al mismo tamaño que en la realidad.

Escala de ampliación:

Se utiliza cuando el objeto representado es muy pequeño o muestra detalles muy pequeños. En ella del numerador es siempre mayor que el denominador.

Puede haber multitud de escalas, por ello se ha establecido una normalización en el uso de éstas.

La norma que regula las escalas a utilizar en los diferentes campos de la industria es UNE-EN ISO 5455:1996.

En el cuadro de abajo tenéis las más utilizadas en cada campo:

Ejemplos prácticos:

EJEMPLO 1

Se desea representar en un formato A3 la planta de un edificio de 60 x 30 metros.

La escala más conveniente para este caso sería 1:200 que proporcionaría unas dimensiones de 30 x 15 cm, muy adecuadas al tamaño del formato.

EJEMPLO 2:

Se desea representar en un formato A4 una pieza de reloj de dimensiones 2 x 1 cm.

La escala adecuada sería 10:1

EJEMPLO 3:

Sobre una carta marina a E 1:50000 se mide una distancia de 7,5 cm entre dos islotes, ¿qué distancia real hay entre ambos?

Se resuelve con una sencilla regla de tres:

si 1 cm del dibujo son 50000 cm reales

7,5 cm del dibujo serán X cm reales

X = 7,5 x 50000 / 1 … y esto da como resultado 375.000 cm, que equivalen a 3,75 km.

Escalas Gráficas:

La escala gráfica o escala volante es una escala dibujada en el papel. Esta escala puede ser ampliada o reducida respecto a las medidas reales del objeto según conveniencia. Las medidas se toman en el objeto con la regla real, pero se dibujan en el papel según la escala fabricada.

La contraescala es una división de una de las unidades de la escala gráfica en unidades más pequeñas, generalmente en décimas.

Ejemplos de diferentes escalas gráficas. La tercera con contraescala.

La escala gráfica se aplica utilizando el teorema de Tales, colocando de una parte las unidades del dibujo y en la otra las unidades de la realidad.

Véase, por ejemplo, el caso para E 3:5

1. Con origen en un punto O arbitrario se trazan dos rectas r y s formando un ángulo cualquiera.
2. Sobre la recta r se sitúa el denominador de la escala (5 en este caso) y sobre la recta s el numerador (3 en este caso). Los extremos de dichos segmentos son A y B.
3. Cualquier dimensión real situada sobre r será convertida en la del dibujo mediante una simple paralela a AB.

Escala Transversal:

Se diferencia de la anterior en que además de décimas de unidad podemos apreciar centésimas de unidad.

Ejemplo de Escala Transversal

 

Triángulo Universal de las Escalas:

Es un triángulo en el que podemos encontrar las escalas más utilizadas.
Lo haremos mediante un triángulo equilátero cuyos lados midan, por ejemplo 10 cm, o bien mediante  un triángulo rectángulo cuyos catetos midan 10 cm.

Además de las escalas gráficas existen los escalímetros que son reglas con diferentes escalas para poder trabajar sobre el dibujo con ellas.

El pie de rey es un instrumento que se utiliza para tomar las diferentes medidas sobre el objeto real a representar.